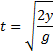After reading a Built on Facts post on a recent Mythbusters episode that tackled one of the classic first year physics problems (that I happen to be TAing right now), and posting the video on my Facebook, one of my more analytic friends pointed out the shoddiness of the 10% error in their precise experiment.
First, here’s both parts of the video, the first contains all the numbers you need to run the physics estimates and the second has the results:
Here’s the summary of the important values:
- Horizontal distance (fired outside): 360 ft = 110 m
- Vertical drop: 36” = 0.914 m
So let’s run through the calculations and see where some error can accumulate.
First source: They measured the horizontal distance outside and then moved the gun inside and never re-measured the horizontal distance. While the calculations don’t tend to care where the gun is fired (since we ignore air resistance), the actual bullet is potentially affected by the wind/weather/etc. outside. Humidity actually decreases the density of air, creating less drag and friction than drier air. Total error (estimated): ~0.5%
Second source: I’m not sure if this is a source of error, since information was omitted, but they never guaranteed that the gun was fired level outside when they shot it to find the horizontal distance. Since the bullet needs to leave the barrel with zero vertical velocity, it is imperative that the gun be fire horizontally. However, this ranging exercise was more to place the dropped ball at the same spot as the bullet for the camera, so I’m going to take this error as negligible (however, this distance becomes important for my later calculations, but we’ll assume it’s within ~5%, or about 5 m of the reported distance).
How long should the drop take until the bullet (or ball bearing) take to hit the ground?
with g=9.81m/s2, the acceleration due to gravity near the surface of Earth, we get a drop time of 0.432s. Just under half a second, or about the time your mind takes /to comprehend a simple picture.
Since we know the time to drop (or at least the theoretical value since they didn’t tell us the experimental time), we can calculate the horizontal velocity.
where x is the total distance of the bullet, measured outside. This gives a velocity of 255 m/s leaving the barrel, or 3/4 the speed of sound.
Third source: I’m not too familiar with fluid dynamics, but suffice it to say that we can assume some difference in downward drag between the bullet and the ball bearing, although unlikely to account for much more than a 1% error.
And if you really want to get technical with a discussion of fluid dynamics, drag and models of bullet ballistics, check out the overly-in-depth Wikipedia article on ballistics as a start.
Now, in part 1, Adam uses a laser to make a line, level with the gun, at a sheet 20’ from the barrel. He then claims that the bullet’s drop between the gun and the sheet will be negligible. It’s worth noting that we expect this to be false since the distance between the sheet is roughly 1/20th of the total distance travelled, or 5%.
Since we know the horizontal velocity (or at least have a calculated estimate of it), we can find the distance dropped in that distance via the time. Rearranging equation (2) to find the time, we get 0.0239s to hit the 20’ target and rearranging equation (1) to find the drop, y, we get a drop of 2.39 cm, or almost 1”.
Fourth source: Adam assumed that in the first 20’ of horizontal travel that the bullet’s drop was negligible when in fact it represented 1/36 of the total drop of the bullet. This introduces an error of roughly 3%, not huge, but it’s beginning to add up.
Now, Jamie show’s off his impressive timing device and demonstrates that the release is timed to 1/3 of a millisecond, or 300 microseconds.
Fifth source: The timing difference introduces an absolute error of less than 1%.
However, to demonstrate his device, Jamie places the dropper and the gun next to one another and lets the high-speed camera capture the release difference. He then moves the dropper to the end of the course for the actual test. I have to assume for safety that they coiled the long cord up when they had the two devices next to one another. A coiled wire will have some inductance, and hence an associated time constant, which will delay the signal. This would mean that the ball might drop sooner when the wire is straightened out.
Let’s figure out an order of magnitude for this time constant.
The inductance of a coiled wire is given by:
Where L is the inductance, is the permeability of free space, N is the number of loops, A is the area of a loop and l is the length of the coil (assume this to be 10cm for a tight packed coil, note this is not the length of the wire). The wire has to be at least 360’ long, and they likely coiled the majority of it, and if it is coiled into loops with area of 0.785m2 (assuming loops of 1m diameter) we therefore have 32 loops. Using all of this we get an inductance, L of 10.1 mH. If we assume resistance of the wire to be 0.1 Ohms, then we get an RL time constant of up to 0.1 s.
Sixth source: If Jamie coiled the wire of his dropper when he measured the two devices next to one another, he may have introduced a significantly large time constant into the system – on the order of the time it took to drop the ball! Since I don’t know whether or not this happened, or to what extent, I can’t quantify this error any better than to say it could be negligible if it was controlled for, or it could have screwed the experiment. Of course, with properly shielded cable this may not even be a concern.
I have just a couple more issues:
Seventh source: The shutter speed of a high-speed camera is finite, so they have an upper limit on measurements taken by the camera. The best guess I have for this is the 300 microsecond measurement that they gave for the measured difference in the drop times, assuming that measurement was limited by the camera. Knowing Mythbusters, I can see them having some of the fastest high-speed cameras that are commercially available, so this error is likely negligible.
Eighth source: I almost forgot this one, but it’s a huge no-no in science. They got cocky and ran their experiment only once! Their trigger device still worked, so the least the could have done was performed a couple times and averaged them out (perhaps they did and it didn’t make the cut). This is just sloppy and it’s hard to really quantify any error with this though.
Taking all of these various sources, especially the incorrect drop assumption (fourth source of error) and potentially the cord inductance (sixth source), it is not unreasonable that the difference could be upwards of 10% in this experiment.
Of course this is Mythbusters and not a class on error analysis. The show is more valuable by remaining entertaining and employing the rough tools of science, with the nitty-gritty details to be filled in later.