Since moving to the UK, I’ve been interested in what’s called the "coin-change problem." Simply put, it comes down to what is the best set of coins that minimizes the number of coins in my wallet.
Canada currently has 5c, 10c, 25c, $1, and $2 coins (having recently eliminated the penny), while Britain and Europe have 0.01, 0.02, 0.05, 0.10, 0.20, 0.50, 1 and 2 coins (in their respective currencies).
The problem appeals to my random interests in applied mathematics and programming (aka engineering) but it turns out to be just slightly beyond what I can do now (I’ve likely forgotten some of the better tricks to solve this).
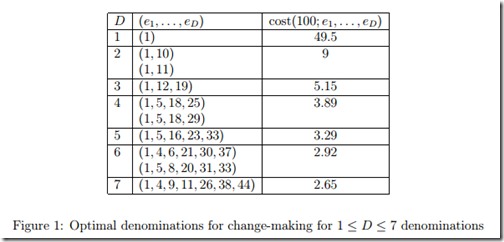
Luckily, the internet provided me with a link to University of Waterloo’s Jeffrey Shallit’s paper where he solved the problem for various cases in 2003.
For currencies that need to spend up to 99c, he found the following optimal change mixtures.
At the time, Canada and the USA both had the same 4 coins under $1, but should have changed dimes out for 18c piece. Interestingly enough, Shallit also determined that the best improvement to both country’s coin systems would be the introduction of an 18c piece.
Europe and the UK both have 6 coins worth less than a Euro/Pound but neither come close to the optimal system.
The mathematical analysis obviously makes a few unjustifiable assumptions. First, as Shallit points out, prices aren’t equally likely to end in every digit from 1 to 99. More importantly though, this approach assumes that people are equally as good at adding any set of integers together, which is hardly true. Even I couldn’t easily count by 18s and 29s. But perhaps the introduction of such an unorthodox system of coins would spark a renew a country’s arithmetic skills (or spur the move to electronic payments).
Most importantly though, this paper vindicates my hatred of Britain’s obnoxious 2 pence coin.